One could make a hand measurement of the differences due to sag - with the sled still positioned for one of the lower corner cut marks and the z axis raised, make a mark at the edge of the sled where the longest chain passes over. Then push/pull the sled by hand, away from the distant motor, to put more tension on that chain and make another mark representing reduced chain sag.
Let’s remember the discussion a while back where we were reminded that especially in the lower corners, the direction the sled is traveling makes a measurable difference to the sag. Arriving at a lower corner cut position by traveling up and toward the center would possibly result in a different cut position than coming at it from the middle. There might be a way to get some sag information from those two marks.
Based upon a motor spacing of 3602.6 mm and a sag correction of 27.4, the amount added to left chain’s length to cut 4 (bottom right corner) is 2.6 mm. This is what the formula in the calibration routine calculates (I isolated that part in the code to print out the sag compensation). It’s linear to the sag correction factor, so if your value is, for example twice that value at 54.8, the the additional length would be 5.2 mm (twice as long).
At 3000 mm spacing (~10 foot), all else being the same, sag calculates at 3.8 mm
comparing this with the online calculator I link to above, it seems that our
sag calculation is not correct.
the online calculator does the simple case where the two ends are at the same
height.
when they aren’t, it gets a little more complex
-
figure out the total amount of chain needed to cover the distance
-
figure the horizontal distance covered (based on the chain angle)
-
re-calculate the weight per distance based on the chains weight per length *
total chain used / horizontal distance covered (we should not have to worry
about chain slop here, being off by a link or two won’t noticably add to the
weight) -
now plug the numbers in to the sag formula.
during calibration, we know how much chain we fed out, we know the resulting
distance, we know the chain weight per distance
but we don’t know the tension on the chain (because we don’t know the sled
weight)
David Lang
@madgrizzle
Would it be possible to modify the code so that changes in settings could be updated immediately when the settinds screen is closed?
What i mean is that if you change for example the sag correction or rotation radius… then close settings the sled position would instantly update based on the new calculations. That way you could get instant feedback on the effect of changes.
Also just wondering why the settings are in 2 seperate places, settings and advanced settings? Personally I always seem to open the wrong one first. Lol
I think the settings do get updated. If you got to Actions and select Return to Center, the sled should move after you change settings and then show in the center of the screen. Maybe the view doesn’t update to show it out of place after closing settings? Don’t know.
I think the settings are in two different places because of just the evolution of the software. The original settings you could modify were the ones on the Maslow Settings tab… As things advanced, some settings were added to the Advanced Settings tab. I agree, they could be group differently.
I think it actually should show the change in position right away
That’s exactly what happened. I wish we hadn’t done it that way and I would like to reorganize them but I haven’t found a way to do so without messing up everyone’s settings ![]()
add it to the todo list for a full version release?
I’m so terribly sorry to be that guy who posts without first reading the entire thread, but I saw this and felt it was worth a quick comment… (I also realize this is slightly off topic, please forgive me)
For the record the wood kit has the same number of bars and the same number of pivot joints but does have sleeved fittings (which is technically more parts). Also the tests I did last year showed zero measurable flex under even the highest forces the machine can apply (normal circumstances). Then I stressed the system with a 75 pound sled and still had no measurable flex. Then I increased sled weight until I had over 95 pounds of force on each chain, at that point I was finally able to see flex but it was less than .4mm over the 9 inch bar. Considering that this is nearly 3 times the force that the machine is even capable of exerting on the chains I would say the wooden linkage has “no flex”. Remember, each bar is effectively 3/4" thick 15-ply plywood.
Keep in mind that no matter the material they are made from any consistent slop in a top-mounted linkage will result in the center point of your router being below the tip of your calculated “chain triangle”; on the other hand any consistent slop in a balanced linkage (aka 45˚ linkage) will only result in a different rotational radius, which can be measured and is accounted for when you calibrate.
I looked at the triangularCalibration class definition in GroundControl. I found one thing (maybe others) that looks suspicious. There is a calibrated parameter, “cut34YoffsetEst”. It is a fourth calibrated pararameter that does affect the calibration’s interpretation of the y coordinate of the 3 and 4 cuts. It’s value does not relate to any machine parameters. The reason this is suspicious is: this is a fourth calibrated parameter, and the calibration is only supported by 3 measurements. The calibration needs at least 4 measurements to calibrate 4 values.
I just recently calibrated my machine, going through the default Triangular Calibration steps. I ended up with some of the longer vertical measurements being 9 mm off, which is quite a bit. I am suspicious of the last calibration step. I think it is introducing errors. I think I will be better off avoiding that step all together. I would like to do a calibration benchmark with the calculated rotation radius (138 mm) and y motor offset. Does anyone else done this?
My understanding is that “cut34YoffsetEst” is basically a fudge factor that allows the routine to come to a solution. If that wasn’t there, you would likely never reach the desired error level to exit out of the calibration loop. What that value actually is at the end of calibration is an indicator of how well the calibration model matches your machine… however, I don’t think that number is reported.
If your machine is way off (9mm is way off), then check to make sure your top beam is level, motor mounts are secure (don’t flex), router bit with the ring kit (assuming you are using it), etc.
We know the current calibration routine is not correct, but we have not figured
out what the correct math for it is. Please go through it and make suggestions.
David Lang
Has this been considered?
Using a radius centered at each sprocket with the 2 converging at the bit? Gets rid of triangular mathamatics in my mind but maybe I,m not thinking deep enough. Its simpler in my head at least. Am I being too simple? lolI don’t understand how you would use this.
Don’t you still need to figure the distance between the sprockets and then
calculate the triangle to figure out where you are?
Distance between sprockets yes, but with that the radius’s (radii?) can only possibly converge at 2 points. The top point can always be ignored because it will always be off the work area. Therefore there is only one possible location the bit can be at using the radius method. Make sense or no? The way I see it it would avoid calculating any angles?
This page sets up a couple calculators and the general formulas, it does look like that would eliminate the trig functions. Certainly, avoiding the Arduino trig functions would be an improvement, it could make fixed point calculations easier to do and avoid the Arduino floating point limitations.
you still need to figure out the angle because the chains don’t pivot at the top corners, they are wrapped around sprockets and depart the sprocket at a different place depending on the angle.
as long as the locations are stored in floats we will have problems,our range of positions is just too large.
Could you make a stationary slot/gate for the chain to pass through so the feed point stays stationary? Two rollers perhaps an inch or so from the sprocket?
no, it will always have some variation of here it bends, you can’t have a chain
bend at a perfect point.
David Lang
I will try to explain my understanding of the “geometric chain length”.
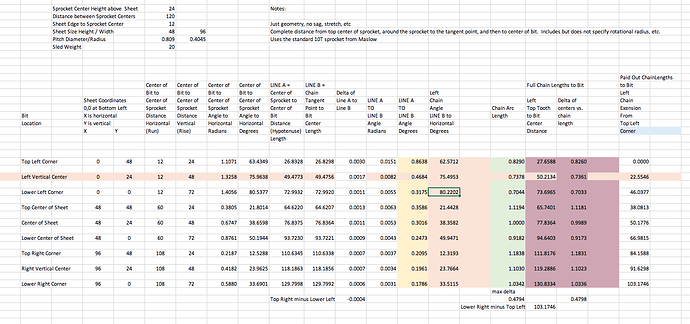
Knowing the “distance” from the “bit center” to the center of the “sprocket”, or intended distance, is the first part of the calculation. This is expressed as the horizontal distance (run) and the vertical distance (rise) in the attached spreadsheet.
This spreadsheet is set at 120" between sprocket centers, 24" above a 48" by 96" sheet, which is “centered”.
You can change these two values to whatever your machine is.
This spreadsheet calculates the 9 key points of corners, sheet edge centers, and center of sheet.
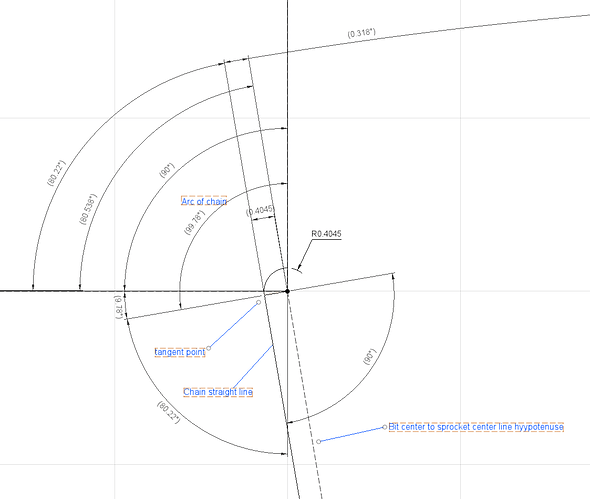
So for any of the 9 points the distance between centers is the hypotenuse of the rise and run, (columns F and G) and the angle to horizontal is the atan of those values (Columns H radians and I degrees). Column J is the distance from the center of the bit to the center of the sprocket (Line A)
Looking at the attached sketches, the hypotenuse is the long dotted line, and the angle is shown.
The sprocket has a pitch diameter of 0.809, radius of 0.4045 for the standard Maslow 10T sprocket.
We can calculate the length of the (line B) from knowing the hypotenuse, radius, and that the chain is tangent (90 degrees) to the sprocket . This is done in column K.
Just for the fun of it Column L is the difference in the lengths of those two distances. Not too much, but counts in the totals.
Next to calculate the angle between the Line A and line B using the asin, knowing the hypotenuse, radius of the sprocket is shown in Column M in radians, Column N in degrees.
Column O shows the angle in degrees of the tangent line B to horizontal.
Looking at the sketch this is the same angle value as the number of degrees of chain wrap around the sprocket below horizontal on the left side of the sprocket. Add to that value 90 degrees for the top left quadrant (always covered with chain) and take that summed value as a ratio to 360 degrees on the circumference and you get the length of chain wrapped around the sprocket from top dead center to the tangent departure point. This is Column Q. At the bottom of column Q I show the difference in max and min chain wrap, for this example -.4794". almost a half an inch. It counts as a significant calculation when the tolerances we are trying to achieve is so much less than that.
Next Column R sums the straight length and wrapped length to give the desired result, the geometric distance of the chain from top dead center to the center of the bit. (all inclusive of various parameters in the code, such as rotational radius, and whatever else is in there. I don’t know code.)
And again just for the fun of it, Column R is the difference between the center to center distance (Hypotenuse) and the derived value for chain distance.
Column U simply shows that if you say the top left corner is “0” inches of chain, how much more chain needs paid out to reach the other 8 points.
Hope this helps to understand the “distance” of the chain.
This does NOT include any of the values that the guys are trying to calculate for chain sag, chain stretch, etc. This is just geometry FYI.
PS. You can play around with varying the height and width dimension a little bit, and you can see the errors it would create if these were wrong. On a piece of plywood, where you are approximating the center to start, would not be a big deal, but when we put a grid on the sheet, and run all of those optical measurements, it really counts to be correct with the settings.
Maslow Chain Lengths Study 2.xlsx (17.1 KB)
Let me know if you see any errors.
The biggest sources of errors are the things we haven’t addressed. We are trying to solve the issue using the same knobs that we’ve already mastered. The current triangular calibration calibrates the known measurements to compensate for unknown measurements. It is no wonder we are getting unpredictable results.
Here is my list of the biggest sources of variation that haven’t been correctly addressed by the current calibration:
- Chain Tolerances
- It is my understanding that the chains are ± 6 mm over their length. This is a huge source of variation.
- Distance Between Motors
- The reason this is on the list is because this needs to be measured to within 0.2 mm to achieve 1 mm accuracy
- Chain Sag
- Even though this is addressed in the calibration, I don’t think the calibration of this parameter is working.
- Chain Stretch
- Frame Flex