This may help. Just my initial simplified analysis.
I, too have been working on a linkages concept, dabbling with it for a few weeks, in fact. I don’t think a four bar linkage will work. I created a spreadsheet which calculated a goodness-of-fit with four bars and then optimized the bar lengths and still came out with the line considerably away from the bit at some places in the arc. I think the pantograph approach is an interesting one. I agree that this may get too complicated an thus be a poor solution, but the ring and pulleys approach isn’t exactly trivial, either. Moreover, since Maslow is aimed at a low-budget / limited-tools user, there are some advantages to a linkage in that bars could potentially be cut on the Maslow. Besides, any approach that involves bars, can’t be all bad, right @bar?
I went to bed with thoughts of four bar linkages swirling in my head. By the time I fell asleep, I came up with a couple of ways I could potentially improve my analysis of the four bar linkage. I’m in @mooselake country right now, so I will have to wait until I return to mundane country before I implement these, but I will report back to the group.
I would be really curious to see what you’ve come up with! For the life of me I could not think of a way to get any point in a “standard” 4 bar linkage to trace a piece of a circular arc that did not have an anchor point at its center. (it is easy enough to trace arcs but bars and fulcrums always seem to be in the way of the router bit.)
A standard Pantograph technically has 4 bars, I just added a 5th to mine so that the tip would trace a perfect circular arc.
I still feel like there might be a more elegant way to solve it with cheap linkages… I have some ideas still. If any turn out to be viable maybe I’ll post them.
-Logan
I think I have a solution with only 3 bars!!

You can play with it here:
As long as AD is equal to BC and DC is equal to or less than AB then E will always trace a circular arc segment with its center exactly halfway between A and B.
Changing the ratio of AD and CB still results in E tracing an arc however the center gets shifted left or right (and I am not certain it’s still a circular arc, but it does look like it is).
The purple line is the path that E can trace. E would be a chain connection point (this mechanism would probably have to be rotated so that the arc segment that E travels lies where the chain would want to run) E is halfway between D and C.
EDIT: I think technically this is a 4 bar linkage because the router base acts as the 4th bar… But it uses only 3 moving bars…
Could you post a sketch of how this connects with the sled, motors, and chains? I am not familiar with using linkages in this way, so am having trouble envisioning how this setup would work. I am looking forward to receiving my Maslow in the next batch, and hoping to decide on a sled connection method before it arrives.
Thanks for all the work you are putting into the idea
Wow, that is stupid easy, and at least in my head seems like it would work.
I assume you plan is to stack two of these, one for each chain?
I think I could cut some test arms from plywood and give this a try this weekend.
Here’s a sideways version. This on either side would get the job done. (appologies if there are issues, never used GeoGebra before 
Beat me to it! Thanks! It could even be at a 45˚ angle… It’ll be interesting to feel how it actually works when I make a real one. (Geogebra is also new to me but it’s pretty awesome so far!)
@krkeegan yes, there would need to be two such assemblies, one for each chain.
Point E can also be moved along line segment CD, moving the center of the circle without affecting the shape. This should allow more flexibility when it comes to mounting points.
Another point (pun intended) is that the positions of the points matter, but the shape of the bars doesn’t have to be a line as long as the shape is rigid and the points are placed correctly. This could help us design around the router and other parts.
Certainly in the sideways version this would be important. As when the sled is all the way to a side, the lower bar linkage arm would need to run through the router. Similarly in the original version, moving the sled to the top of the board might also cause an issue.
Hopefully some version of a 45 degree angle resolves the need to using bent arms.
I just did some more testing and found that while the drawing I posted is REALLY close to perfect, apparently the only time the distance from the center (unlabeled in my drawing) and E remains constant is if AB and DC are also equal lengths. Basically it needs to be a parallelogram in order for E to trace a true circular arc. My bad.
It will still work though, just DC needs to equal AB.
Here’s an updated model with the radius from the router bit to the chain-end labeled so you can mess with lengths and see how it affects the arc. I also rotated it 45˚ to help envision how it could be installed. Drag D around to see the movement, adjust the segment lengths in the panel to the right.
https://ggbm.at/VDVeGhym
As when the sled is all the way to a side, the lower bar linkage arm would need to run through the router. Similarly in the original version, moving the sled to the top of the board might also cause an issue.
Actually, since Maslow’s motor arms are above and beyond the edges of the cutting surface I don’t think the sideways version would be a problem in real life. The router/sled is never directly below either motor. My mind likes the 45˚ look but that would require two bars to actually cross each other, which could be done but adds complexity.
There may be another combination of lengths that produces a perfect arc for long enough for our needs. As has been mentioned in this thread already, there is no need for a full circle or even half a circle. Two relatively short circular segments would suffice. If we can get a linkage to trace a proper arc for just the needed sections we’d be fine.
We won’t need to pivot more than 90 degrees, the chain is never directly above or directly to the side of the sled. If anyone with a Maslow and a protractor wants to figure out the exact angles needed by measuring at the corners, that might help (probably also possible to approximate with drawings/videos if I have time later). We’d also need to add a little bit of slop to account for rotated sleds, so maybe ~90 degrees is a good starting point…
To get around the overlap issue, I see a couple of possibilities. There may be an angles other than 45 degrees that won’t see significant overlap for our <90 degrees of motion. Or maybe we could have different lengths (AB/CD and/or AD/BC) for the left & right sides. As long as the ratios are right, size shouldn’t matter. (not sure if this is what you meant).
I won’t have my Maslow until November, but I may have to pull out the cardboard and scissors and play around with bar configurations 
So, at what point is the chain connected? I’m still having a hard time envisioning this. I think I may just have to wait until someone implements it to see what it looks like. I am sure once I see it, it will be obvious.
Though, for now, I think I am still leaning toward the simplicity of the arc with v-pulleys. I also like the idea of being able to adjust the height of the arc to match the “height” of the motors above the work surface, which I am thinking could be easily accomplished with long bolts and nuts to hold the arc in place.
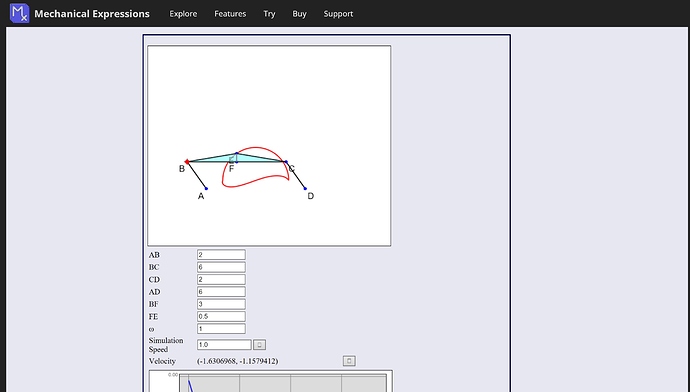
This site is much easier to use than Geogebra…
http://mechanicalexpressions.com/explore/kinematics/4-bar-linkage.html
To help demonstrate what I’m talking about:
The angles are based roughly off a screen capture of Bar’s smaller ring test, it was the most extreme chain angles in the video. There are probably some more extreme circumstances than this but you can see there’s still quite a bit of clearance.
The light grey circle shows the path the chain tips are allowed to travel on and the dashed red lines prove that this is indeed a large triangle with the point being at the center of the router bit. Of course my scale could be way off, there is a lot of flexibility in this design and it’s accuracy should remain pretty solid. Again, this is totally untested but I believe it would prevent jumpy chain rollers and cost much, much less than bearings and rings/rails (I still really like the bearing and rail idea!!!)
To answer your question @Keith, this could be mounted off the platter wherever you wanted. Mounting it away from the surface would be no more complicated than mounting a ring away from the surface (actually probably less complicated since there are only two attachment points).
That’s cool! Is there a way to calculate the center point of that arc? Or a way to prove that it’s a circular arc (equal radius at given points on the arc)?
Very cool tool, much easier to quickly see visual results.
This is a REALLY cool idea, and so well explained!
To stoke the flames further, I bought some of those SailRite steel hoops (the 12" seems to be the best, thanks @Nathan_Miller )
My home bent ones weren’t true circles enough, but with the professionally made ones I had almost no trouble getting my machine calibrated to give me straight lines and the correct distances to as close as I could measure. WAY easier than calibrating with the fixed anchor points system.
I fixed a bug along the way, and now seems like all the firmware/software to test these virtual center pivot systems is in place.
I’m working with our metal manufacturer to try to put together the parts for a bearing and rail system, but it might turn out that you guys get an awesome linkage system that could probably even be cut by Maslow worked out before we can even get anything made.
In either case, the software needed is in place and ready! If anyone is testing one of these systems and having any software trouble, let me know!
Here’s what the setup I was testing today looks like: